本四十四弹为金鹰优化器,而审时言吾嫌广营销,费力作久,无奈只除。汝听!人言否?甚为人心!则离谱!岂为雕牌代言人乎!?
吐槽归吐槽。本期我们介绍政治优化器(Political Optimizer,PO)。该算法由Qamar Askari 等人于2020年提出,主要模拟了政治的多阶段过程,其中算法将种群划分为政党和选区,通过候选人更新政党领袖和选区获胜者的位置来达到寻优的目的。
原文中先给出了大段的介绍性文字,让我们耐心了解一下:
政治在不同的背景下有不同的含义。党的政治制度可以分为四种主要类型:一党制、两党制、主权制和多党制。此外,也可以通过议会制或总统制来治理国家。作者从这些党制中综合了一些共性,像是政党和选区的概念,政治家和政党的联系、同党政治家的合作等等。多党民主的政治实践是一个复杂的政治过程,涉及社会各个层面,如图1所示:
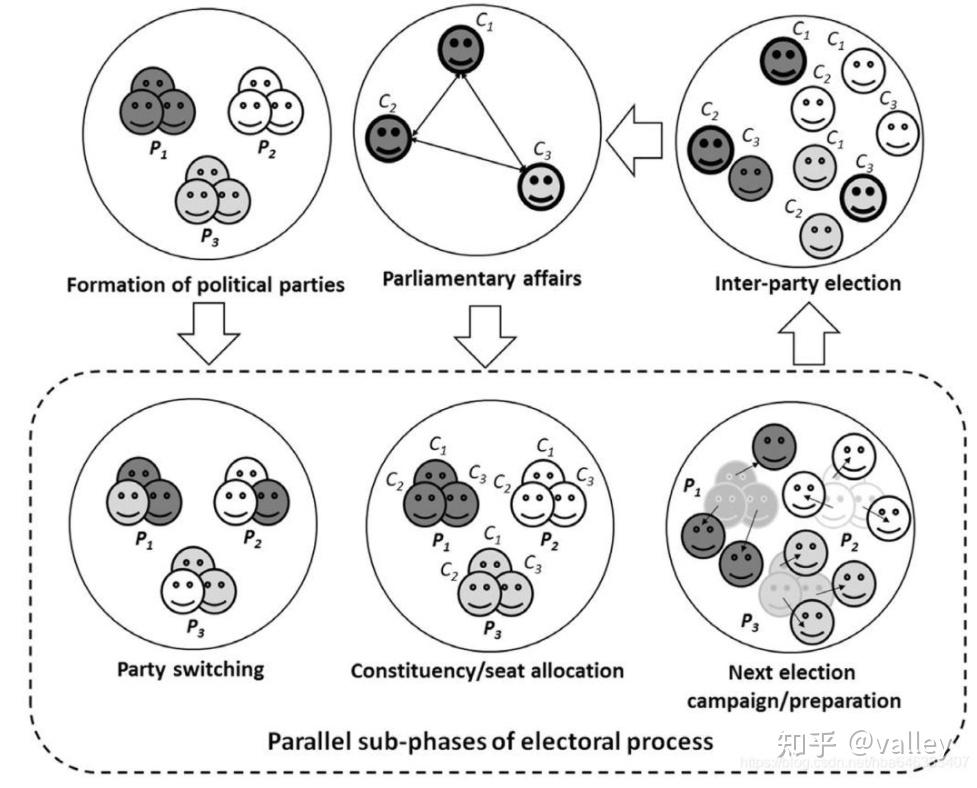
- 政党信息:政党是由具有共同议程的个体组成,这些个体被称为政客或公职候选人,图1中Pi代表第i 个政党的成员。
- 政党选择:成员就根据自己的立场来更换党派,如图1中P1、P2、P3中分别包含了P2、P3、P1的成员。
- 选票分配:成员会被分配政党票,以便在选区中竞争选举。图1中笑脸Ci 表示成员正在进行第i 个选举。
- 竞选活动:候选人查看他们的选区并说服选民投票,这会使候举人的声誉进行更新。
- 党间选举:在每个选区,选民投票给候选人以决定获胜者。图1中每个选取的获胜者加粗表示,如P1在C1、C2中胜出。
- 政府组建和议会事务:来自各党派的获胜者组成议会,并相互合作运行政府。
下面进入正题。PO算法由五个阶段组成,包括政党组建和选区分配、竞选活动、政党转换、政党间选举和议会事务。其中政党组建和选区分配只运行一次,其余四个阶段在循环中执行。
政党组建和选区分配
首先将种群P 分成n个党派:
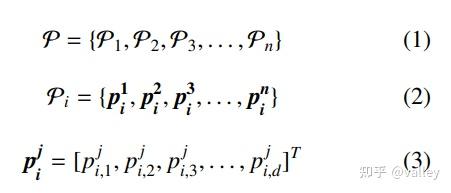
这里每个党派又包含n个成员,d 为空间维度。假设一个党派内包含n个选区:
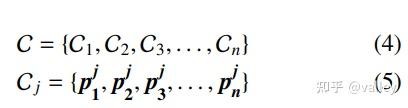
选区和党派的关系如图2所示:
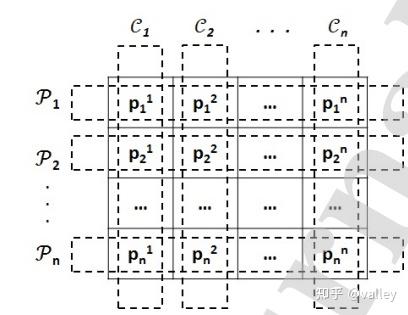
简单来讲就是说p1(1)他是党派1中选区1内的成员。一个党派中人气最高的成员被宣布为党派领导人,这是在大选(跨党派选举)之后决定的:
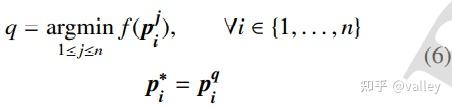
其中pi为党派i 的领导人。所有党派领导人(就是把每个子种群的最优个体集合起来)的集合由P* 表示:
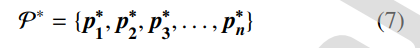
选举结束后,每个党派中所有选区的获胜者成为议员,组成议会:
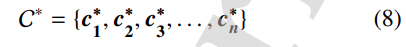
简单来说就是c1* 对应图2中第一列的最优个体。
政党选举活动(探索和开发)
这一阶段有助于候选人提高他们在选举中的表现,若个体i在此代适应度值优于前一代适应度值,则遵循式(9),否则遵循式(10):
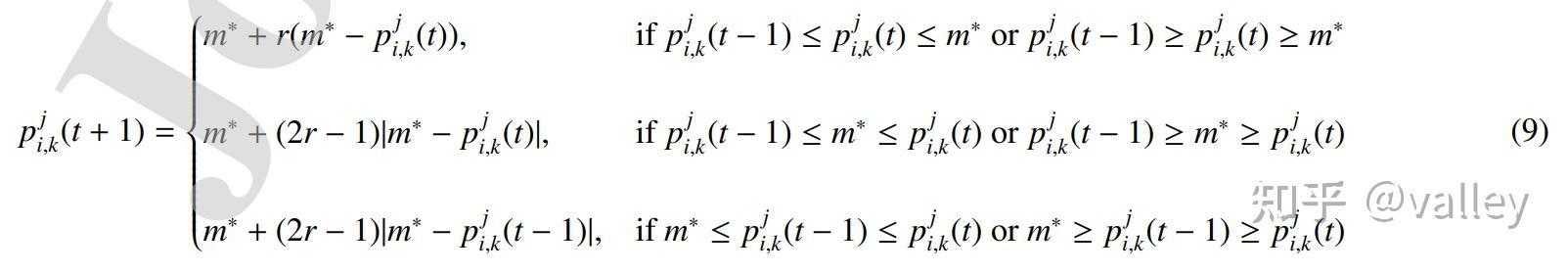
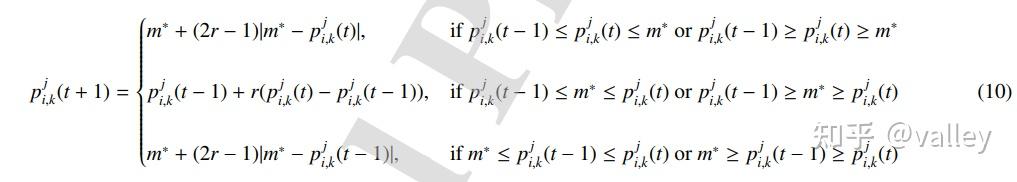
式中r 为[0,1]内一随机值,式(9)中的m* 为所有党派的领导人(全局最优个体),而式(10)中的m* 为议会中的对应个体。可以看出,这六种更新方式都比较一般,没什么花里胡哨的。每一种方式的1、3更新对应探索,2对应开发。至此,此部分的算法迭代伪代码为:

政党转换(平衡探索和开发)
此阶段引入一个名为"党派转换率"的自适应参数 来平衡算法的探索行为、开发行为。每个成员依据
来判断是否随机跳槽到另一个党派(他会和该党派适应度值最差的个体交换以维持各党派人数)。此部分算法迭代伪代码为:

竞选(适应度值评估)
这个竞选,顾名思义,对应算法中的适应度值更新及最优个体选取。
议会事务
在跨党派选举后,政府成立。这里也就是人员的更替,不过涉及了cnew这么个变量:

至此,算法整体介绍完毕。图3为假设n=3情况下算法的操作流程:
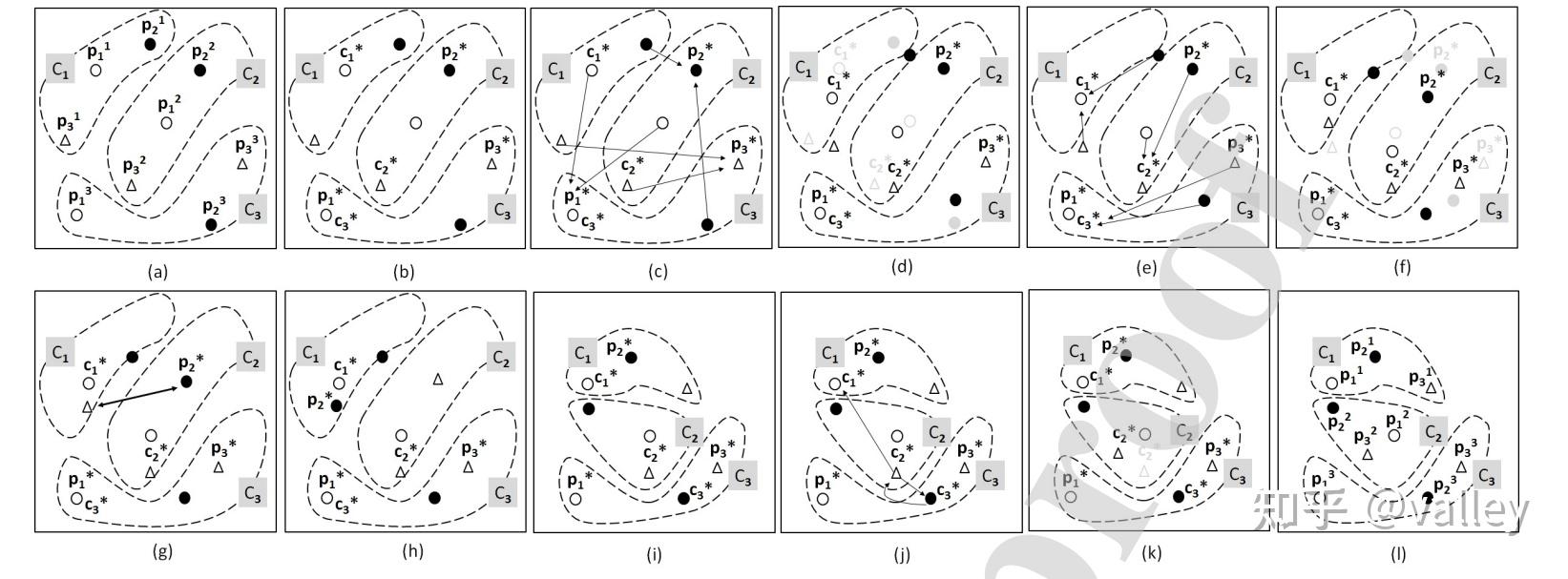
图3中虚线区域表示选区,每个党派的成员用不同的符号表示。
(a).种群初始化
(b).选举产生党派领导人和选区的获胜者。
(c-d).根据党派领导人更新位置。
(e-f).根据选区获胜者更新位置。
(g-h).政党转换。
(i).选举阶段、党派领导人和选区获胜者角色的重新分配。
(j-k).议会事务阶段。
(l).重新生成位置。
算法总体迭代伪代码为:

本期我们将PO算法与往期的冠状病毒群体免疫优化器(CHIO)、蜜獾算法(HBA)在部分CEC2017测试函数上进行对比测试,取种群规模为30,维度为30,最大迭代次数为10000,计算结果如下:
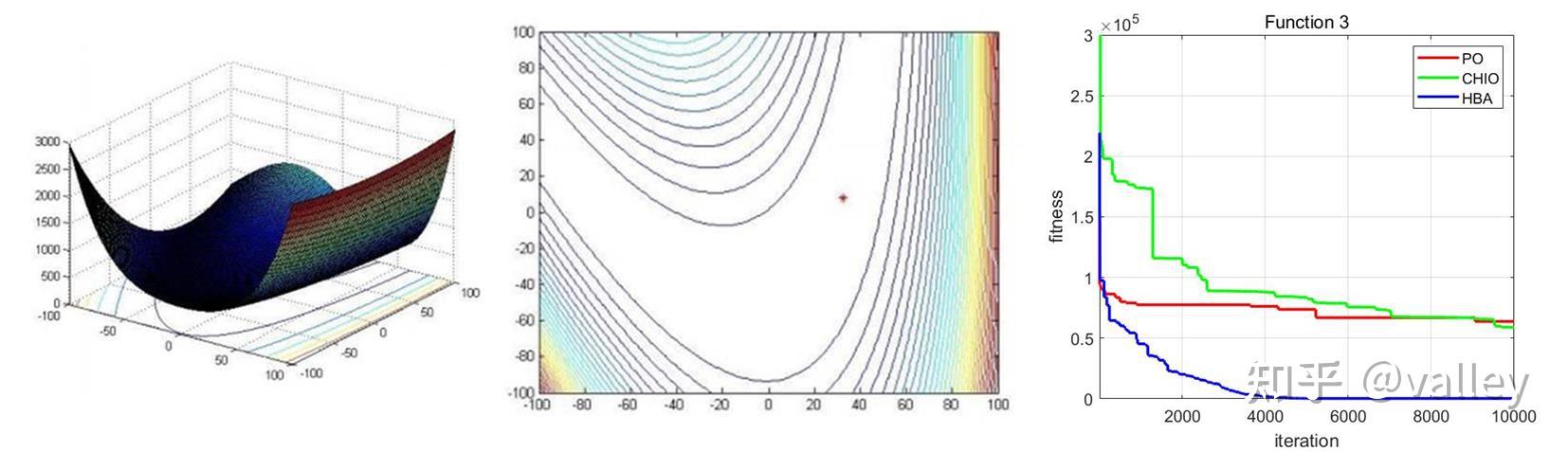
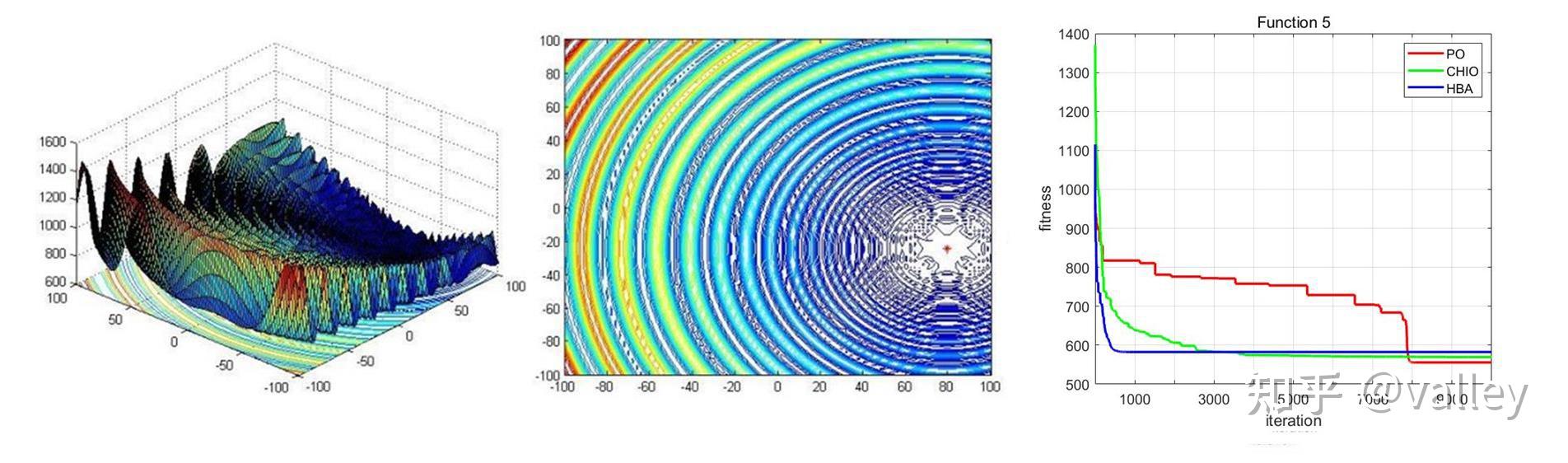
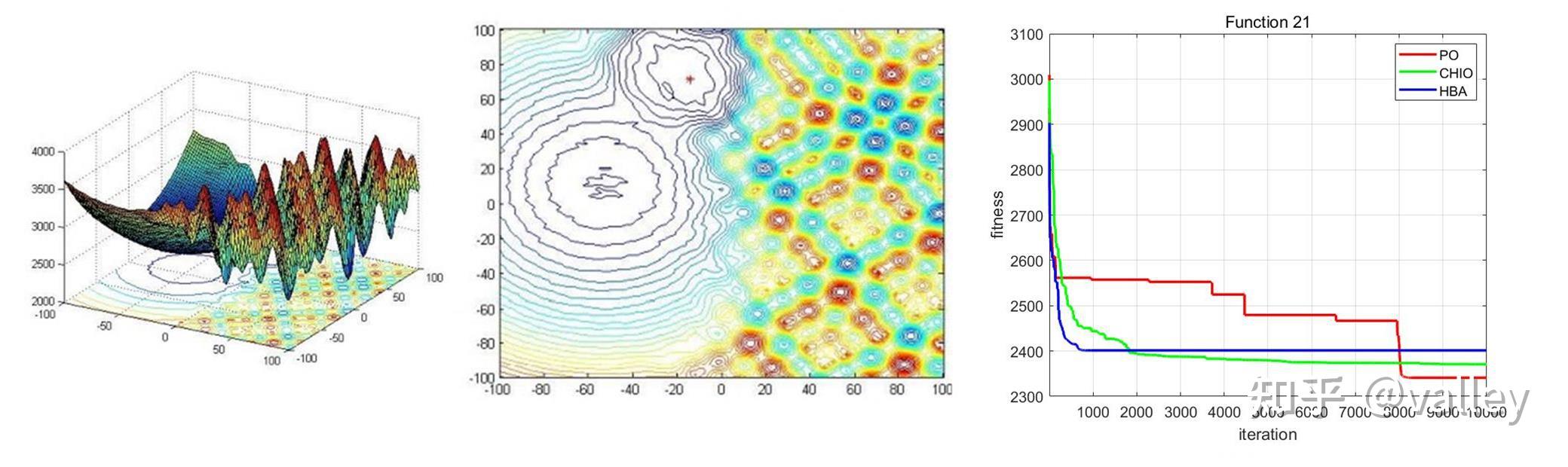
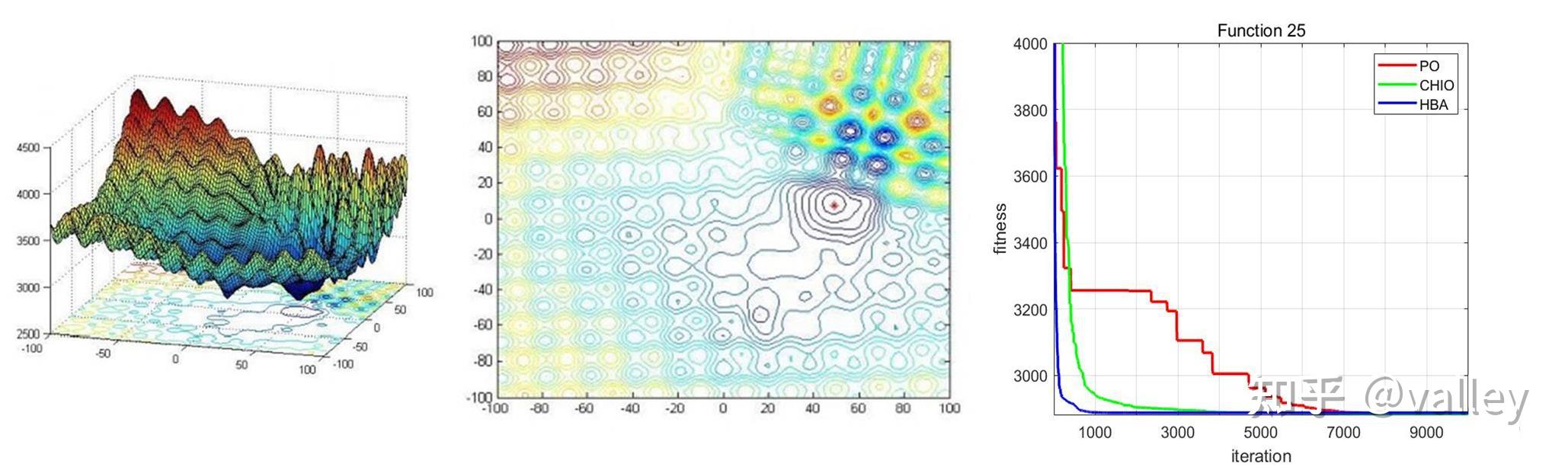
就迭代曲线来看,PO算法虽然精度不容置疑,但这个收敛速度属实拉胯啊。。。在原文中的标准测试函数测试上PO算法的性能也不错:

总体来说,PO算法结构较为复杂,但是理解了相关概念后就比较容易上手了。算法从逻辑上将种群划分为政党和选区,为每个成员分配双重角色。因为有多个较优解,所以在议会事务阶段成员间相互交流,进一步提升议员的质量,同时政党选择操作也提升了次级种群多样性。但是这就产生了较大的运算量,而且收敛速度欠佳。期待更多的改进版本~


